Qual a diferença entre juros simples e juros compostos?
O tipo de juros é determinante para o custo final. Entenda as diferenças para tomar a melhor decisão
Os juros funcionam como um aluguel cobrado sobre o dinheiro emprestado. Podem ser de diversos tipos. Aqui, vamos falar dos juros simples — que, como diz o nome, são mais simples de calcular —, e dos juros compostos — também chamados de juros sobre juros, bem mais comuns no mercado. Siga a leitura e entenda as diferenças entre os dois:
Juros simples — A modalidade mais objetiva
A principal característica que diferencia os juros simples dos demais é a maneira como ele é calculado. Os juros simples são uma taxa fixa que incide sobre o valor inicial do contrato e é dividida durante a duração do contrato.
Veja no exemplo:
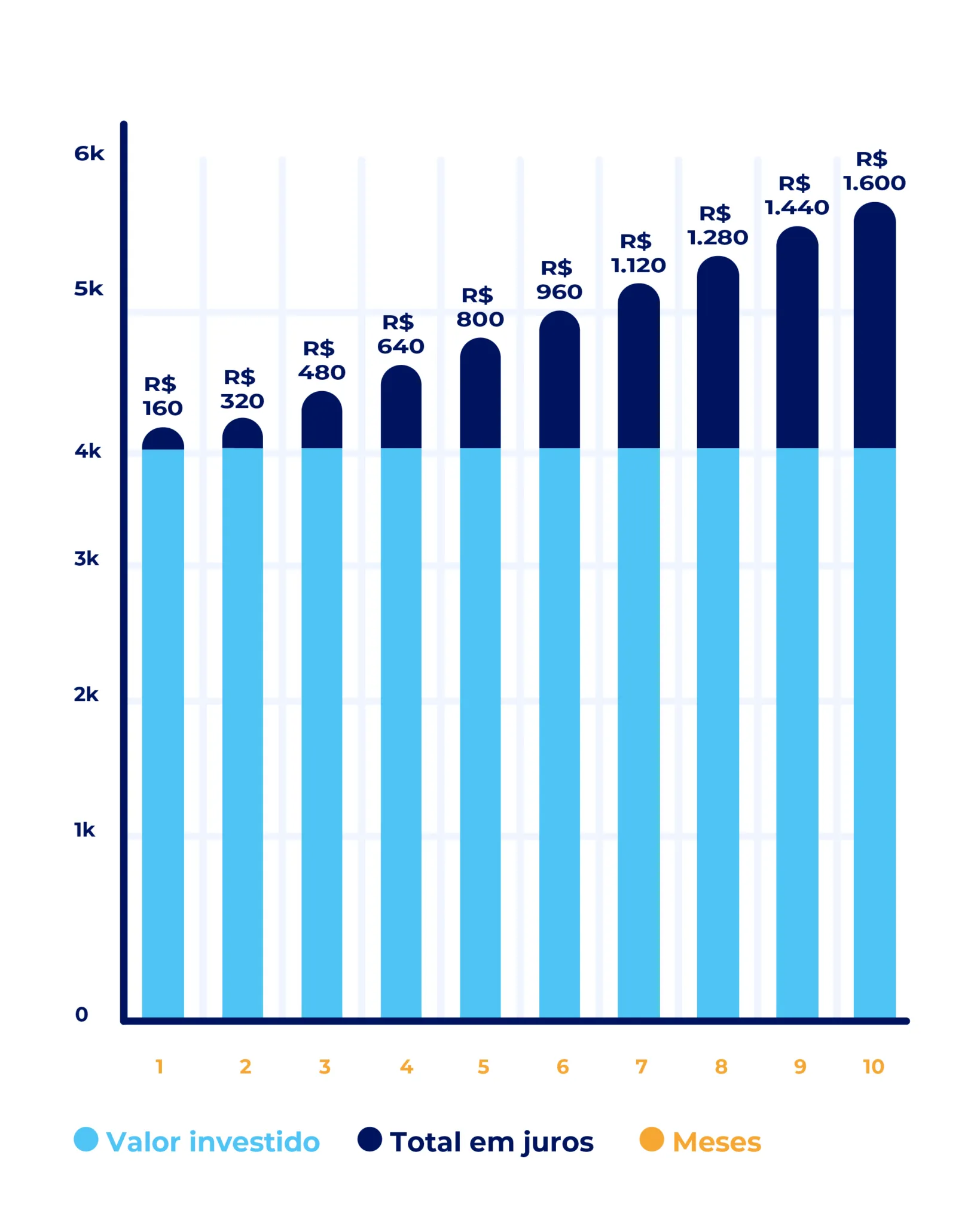
Laura fez um empréstimo no valor de R$ 4.000, com juros de 4% ao mês, e precisa pagá-lo ao longo de 10 meses. Com isso, ela terá que pagar uma parcela (R$ 4.000/10 = R$ 400), mais o acréscimo de R$ 160 (4% de R$ 4.000) todos os meses.
No final do período, o acréscimo final de juros seria de R$ 1.600. Ou seja, o valor total do contrato seria de R$ 5.600. Aos R$ 4.000 iniciais, seriam somados R$ 1.600 de juros.
Apesar de ser uma modalidade mais objetiva e simples de juros, é pouco usada tanto em empréstimos como em investimentos. As taxas mais usadas são as compostas, calculadas de forma diferente.
Juros compostos — O mais utilizado
Os juros compostos são a modalidade mais recorrente de juros, e são comumente usados quando uma pessoa investe ou pega um empréstimo. CDB (Certificado de Depósito Bancário), LCI (Letra de Crédito Imobiliário) e LCA (Letra de Crédito do Agronegócio) são alguns exemplos de investimentos que trabalham com juros compostos.
Os juros compostos são também conhecidos como “juros sobre juros”. Nessa modalidade, os rendimentos – ou a dívida – são calculados não apenas a partir do capital investido ou emprestado inicialmente, como acontece com os juros simples, mas também sobre os ganhos de todos os períodos anteriores.
Veja no exemplo prático:
Exemplo de cálculos com juros simples e juros compostos
Se aplicar R$ 10.000 a juros simples, com remuneração de 1% ao mês, durante seis meses este será o resultado:
- 1° mês: R$ 10.000,00 x (0.01) = R$ 100
- 2° mês: R$ 10.000,00 x (0.01) = R$ 100
- 3° mês: R$ 10.000,00 x (0.01) = R$ 100
- 4° mês: R$ 10.000,00 x (0.01) = R$ 100
- 5° mês: R$ 10.000,00 x (0.01) = R$ 100
- 6° mês: R$ 10.000,00 x (0.01) = R$ 100
A cada mês conseguiu-se R$ 100 a mais e, ao final do período, o rendimento foi de R$ 600 no total.
Agora veja como seria com juros compostos, dentro das mesmas condições iniciais (aporte e taxa de juros):
- 1° mês: R$ 10.000,00 x (0.01) = R$ 100
- 2° mês: R$ 10.100,00 x (0.01) = R$ 101
- 3° mês: R$ 10.201,00 x (0.01) = R$ 102
- 4° mês: R$ 10.303,01 x (0.01) = R$ 103
- 5° mês: R$ 10.406,04 x (0.01) = R$ 104
- 6° mês: R$ 10.510,10 x (0.01) = R$ 105
Neste caso, a cada mês, o valor foi aumentando um pouco mais, e o total no período foi de R$ 10.615,20, ou seja, com R$ 615,20 de ganho. R$ 15,20 a mais que a aplicação em juros simples.

Vantagens e riscos dos juros compostos
Os juros compostos podem ser grandes aliados na hora de fazer um investimento já que têm a capacidade de multiplicar os rendimentos aplicados.
Porém, eles nem sempre são bem-vindos quando se trata de empréstimos ou dívidas, como atrasos de contas. Neste caso, é preciso redobrar o cuidado, porque os juros vão aumentar progressivamente o valor devido pela pessoa tomadora do dinheiro, ou devedora.
Veja um exemplo:
A fórmula dos juros compostos é “montante igual ao capital inicial vezes um mais a taxa de juros, elevado ao tempo“.
M = C x (1+i)^t
Sendo:
- M = montante (resultado)
- C = capital inicial
- i = taxa de juros aplicada
- t = tempo (duração do investimento)
Podemos pegar um financiamento de R$ 50.000 (C) para pagar em dois anos (T) a uma taxa anual de 12% (I):
- M = 50.000 x (1 + 12 ÷ 100)²
- M = 50.000 x 1,2544
- M = 62.720
Ou seja, ao final de 24 meses você terá pago os R$ 50 mil que pegou emprestado + R$ 12.720 de juros.
Veja agora o mesmo cálculo na fórmula de juros simples, que é M = C + J. Ou seja, o montante final (M) é o resultado da soma entre o capital inicial (C) e os juros (J). Os juros, por sua vez, são calculados pela taxa percentual (i) multiplicada pelo capital inicial vezes o tempo de duração do contrato (t), J = i x C x t.
- J = 0,12 x 50.000 x 2
- J = 12. 000
- M = 50.000 + 12.000
- M = 62.000
Assim, pagaria, no total, menos que o valor final por juros compostos, que foi de R$ 62.720.
Agora que você já entendeu mais sobre como são calculados os juros simples e compostos, aproveite e leia também nosso post a respeito do tema Preço sobre Lucro! Até a próxima!
Para saber ainda mais sobre investimentos e educação financeira, não deixe de visitar o Hub de Educação da B3.














